ええ本当!?そんな方法で宝くじに当選できるの?うそびっくり!!絶対当たる方法とは!?

もったいぶらずにその方法を一番最初にお伝えします。
簡単ですからみなさんも是非試してみて下さいね。
その方法とはズバリ!
全部買う or 当たるまで買う
です!
・・・・・・・・・・・・・・
「ひょっとして本当に宝くじに当たる方法があるのかも!?」
と思って来てくれた方・・・
○| ̄|_ホントウニゴメンナサイ
そして
目を覚ましてください!
そんな方法あるはずがありません、ですがネット上にはそのような胡散臭い情報がたくさん存在しています。
むしろこのページにたどり着けたあなたはラッキーです、そんな胡散臭いサイトからあなたを守ることができて私は幸せです。
・・・・・・・・・・
いや嘘です(笑)
本当はブログのPVが1増えて喜んでいます。
つまり私もあなたもハッピーハッピーのハッピーセットです。
まったくもって意味不明です。
本当にありがとうございました(笑)
せっかくなので宝くじの当選確率や期待値について書き記しておくので、良かったら読んでいって下さい。
宝くじの当選確率
このままではただのタイトル釣り記事になってしまうので(もう十分手遅れ)、宝くじに関する正しい情報を提供して、なんとかブログの名誉を守ります。
まずは宝くじの各等級ごとの当選確率から見ていきましょう。
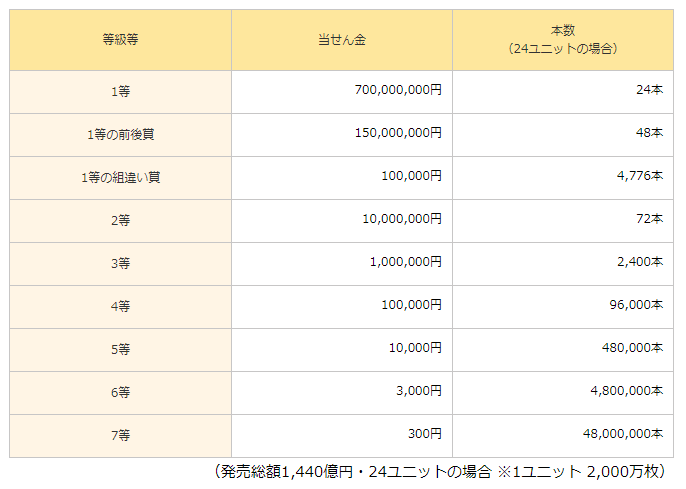
こちらの表は2018年に発売された「年末ジャンボ宝くじ(第770回 全国自治宝くじ)」の当せん金とその本数を表したものです。
当たりの本数に関しては24ユニット分の数になっていますね(少しでも多く入っているように見せる工夫w)
ちなみにユニットというのは組も数字も全く同じもののことで、24ユニットなら「○○組○○○○○○」という宝くじが24つ存在するという意味です。
よく「1等が○○本!」とか聞くのに当選番号は1種類なのはこのためですね。
1ユニットは大抵1000万通りか、2000万通りの組み合わせでできているようです。
今回調べた「年末ジャンボ宝くじ(第770回 全国自治宝くじ)」は、1等賞金が7億円と高額なので2000万通りでした。
分かりやすくするために1ユニット毎の当たり本数と確率を表にしてみました。
| 等級 | 当たり本数 | 確率 |
| 1等 | 1本 | 1/20,000,000 |
| 1等の前後賞 | 2本 | 1/10,000,000 |
| 1等の組違い賞 | 199本 | 1/100,503 |
| 2等 | 3本 | 1/6,666,667 |
| 3等 | 100本 | 1/200,000 |
| 4等 | 4,000本 | 1/5000 |
| 5等 | 20,000本 | 1/1000 |
| 6等 | 200,000本 | 1/100 |
| 7等 | 2,000,000本 | 1/10 |
※確率は小数点以下を四捨五入しています
1等の組違い賞が199本(1本は1等)ということは、全部で200組×100,000通りの数字の組み合わせで2000万通りになるということですね。
賞金が1000万円の2等ですら当選確率は「1/666万」以下です、1枚300円なので約20億円分につき1枚です。
もう一度言いましょう
1000万当てるのに20億です
1等の7億はたったの60億円分買えば当たるのにね(笑)
サイコロで例えてみた

宝くじの1等が2000万分の1とか言われてもまったくもってピンとこないので、身近にある確率としてサイコロを例えに考えてみます。
言うまでもなくサイコロを振って1の目が出る確率は6分の1です。
2つのサイコロ振って両方とも1の目が出る確率は6×6で36分の1です。
これを繰り返して2000万分の1に近づけていきましょう。
サイコロ5個ではどうでしょうか?
6×6×6×6×6=7776
まだまだ1万分の1以上ですね。
サイコロ10個ではどうでしょうか?
6×6×6×6×6×6×6×6×6×6=60,466,176
・・・・・・・・・
すまん行き過ぎた(笑)
まぁでも6の10乗で約6000万てことは、9乗で約1000万(正確には10,077,696)になるということですね。
あとはこれを倍にすればいいだけだからコインでも投げときゃいっか・・・
ということで2000万分の1というのは
サイコロ9個とコイン1枚を投げて全部が1の目とコインの表が出る確率
と大体同じということになります。
(正確には1/20,155,392)
さあ、この条件をクリアできる自信のある方はすぐに宝くじ売り場へGOです(笑)
宝くじ1枚当たりの期待値

宝くじ1枚当たりの期待値を算出してみます。
まずは念のために期待値という概念を説明しておきます。
期待値とは
確率論において、確率変数の期待値(きたいち、英: expected value)とは、確率変数のすべての値に確率の重みをつけた加重平均である。確率分布に対して定義する場合は「平均」と呼ばれることが多い。例えば、ギャンブルにおいて掛け金に対して戻る金額の期待値とは、戻ってくる「見込み」の金額である。ただし、確率変数が期待値を取る確率が最大とは限らず、確率変数が期待値を取るわけでもない。しかし、独立同分布であれば、標本平均は期待値に収束することが知られている(大数の法則)。
もう少し分かりやすく説明しましょう。
例えば全100本中10本だけが当たり、それ以外はハズレというくじがあったとします。
当たりの賞金が1万円でハズレは0円という設定だったとしましょう。
このくじの全賞金額は1万×10本=10万円で、その総数は100本です。
当たり前ですが、100本買えば10万円分当たりますね。
この「100本で10万円分の価値がある」というのが期待値の考え方の基礎になります。
ここからこのくじの1本分の価値を算出すると「100,000円÷100本=1000円/本」となります。
つまりこのくじの1本分の価値は1000円となり、言い換えれば「期待値が1000円」ということになります。
この「期待値を考える」という行為は、確率に左右されるギャンブルにおいて必須となります。
(あ、もちろん勝ちたい場合ねw)
要は上記のくじの場合、1枚当たりの価格が「期待値である1000円より高ければ買うと損」、逆に「1000円より安ければ買うと得」ということになります。
これほど簡単な計算なら誰でもできますが、少しややこしくするだけで途端に分からなくなる、もしくは考えることを放棄する人はごまんといます。
こうしてちゃんと計算をできる人だけが得できるシステムとして誕生したのがギャンブル・・・、だと私は思っています(笑)
1ユニット全部買うと

それでは宝くじ(年末ジャンボ宝くじ 第770回全国自治宝くじ)の1枚当たりの期待値を算出してみます。
まずは1ユニットの賞金総額を計算してみます。
1等=700,000,000円 × 1本 (7億)
前後賞=150,000,000円 × 2本 (3億)
組違い賞=100,000円 × 199本 (1990万)
2等=10,000,000円 × 3本 (3000万)
3等=1,000,000円 × 100本 (1億)
4等=100,000円 × 4,000本 (4億)
5等=10,000円 × 20,000本 (2億)
6等=3,000円 × 200,000本 (6億)
7等=3,00円 × 2,000,000本 (6億)
賞金総額は29億4990万でした。
これを1ユニットの総枚数2000万で割ると147.495となります。
つまり宝くじ1枚当たりの期待値は147.495円ということです。
あなたは147円しか価値のない紙を300円で買いますか?
最後に

こんな釣りタイトルの記事を最後まで読んでくれて本当にありがとうございます。
しかし私が最初に掲げた宝くじに絶対当たる方法「当たるまで買う」というのは、よくある詐欺の手法なのです。
ここまで分かりやすいと誰も引っかかりませんが、すこし複雑にすると引っかかってしまう人がいるのが事実です。
海外では「雨乞い」という職業が成立している国があります、彼ら「雨乞い」は頼めば必ず雨を降らすことができるからです。
その手法というのが「雨が降るまで祈り続ける」というものです。
当然先進国の日本では詐欺はもっと巧妙な手口になっています。
どうかくれぐれも自分で考えるという行為を怠らずに、賢く生きて下さい。
あれ、何の話だったっけ・・・
あ、そうそう、大切な話を忘れるところでした。
実は宝くじの収益は様々な公共事業に役立てられています、よく公園などの設備に「宝くじの収益で作りました」的なことが書かれているのを見かけます。
そう考えれば表面上の期待値は147円でも、それ以上の付加価値があると考えられますね。
社会貢献に役立ち夢も買える宝くじ
あなたは買いますか?
・・・・・・・・・・
いや、あんた買わせたいの?買わせたくないの?
という突っ込みが聞こえてきます(聞こえません)が、私が言いたいことは常に1つです。
自分で考えよう!
ちなみに宝くじの賞金には所得税はかからないそうです。





コメント